地基梁法的推导

在进行路基箱问题的分析时，通过采用地基梁法可实现路基箱对上部荷载的扩散作用进行初步分析。

平衡微分方程

可列出上、下受分布荷载的梁的平衡微分方程 $$EI\frac{\text{d}^4w}{\text{d}x^4}=-bp+q$$ 这里$w$为挠度，$p$为梁底部单位面积向上反力；$q$为梁顶部单位长度荷载；

上述通解为： $$w=Ax^4+Bx^3+cx^2+D$$ 在文克勒地基梁模型中，假定反力与变形成正比例关系，即满足： $$p=kw$$ 这里$k$为基床系数。

则上述方程可以转化为： $$\frac{\text{d}^4w}{\text{d}x^4}+4\frac{bk}{4EI}w=\frac{q}{EI}$$ 这里记： $$\lambda=\left(\frac{bk}{4EI}\right)^{1/4}$$ 求解特征根得到通解为： $$w=e^{\lambda x}(c_1\cos {\lambda x}+c_2\sin{\lambda x})+e^{-\lambda x}(c_3\cos {\lambda x}+c_4\sin{\lambda x})$$ 特解： $$\frac{qx^4}{24EI}$$ 上述用到了线性常微分方程的解。

无限长受居中集中荷载

集中力作用

当假定梁无限长，且仅原点处作用有集中力$F$时，考虑边界条件：

①无限远处挠度为零；

②原点处无弯曲；

③原点处剪力为$fF/2$；

则由①可以得到：

当$x>0$时，即正半轴时，

$c_1$和$c_2$应为0。(否则极限应该是无穷大)，相应有： $$w=e^{-\lambda x}(c_3\cos {\lambda x}+c_4\sin{\lambda x})$$ 相应有： $$w'=-\lambda e^{-\lambda x}(c_3\cos {\lambda x}+c_4\sin{\lambda x})+e^{-\lambda x}(-\lambda c_3\sin {\lambda x}+\lambda c_4\cos{\lambda x})\\=-\lambda e^{-\lambda x}(c_3+c_4)\sin {\lambda x}-\lambda e^{-\lambda x}(c_3-c_4)\cos {\lambda x}$$

由②可以得到： $$w'_{|x=0}=-\lambda(c_3-c_4)=0$$ 相应可得：$c_3=c_4$

则有： $$w=c_3e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})$$ 相应有： $$w’=-2c_3\lambda e^{-\lambda x}\sin {\lambda x}\\ w''=2c_3\lambda^2 e^{-\lambda x}\sin {\lambda x}-2c_3\lambda^2 e^{-\lambda x}\cos {\lambda x}=2c_3\lambda^2 e^{-\lambda x}(\sin {\lambda x}-\cos {\lambda x})\\ w'''=-2c_3\lambda^3 e^{-\lambda x}(\sin {\lambda x}-\cos {\lambda x})+2c_3\lambda^3 e^{-\lambda x}(\sin {\lambda x}+\cos {\lambda x})=4c_3\lambda^3 e^{-\lambda x}\cos {\lambda x}$$

由③得到： $$\lim_{x=0}=-EIw'''_{|x=0}=4c_3\lambda^3=-F/2$$ 则得： $$c_3=\frac{F}{8EI\lambda^3}$$

相关解法里取：$K=bk$为集中基床系数，相应得到： $$c_3=\frac{F\lambda}{2K}$$

$$w=\frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})$$

相应可以得到弯矩，剪力。 $$w=\frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})=\frac{F\lambda}{2K}A_x\\ \theta=-\frac{F\lambda }{2k}e^{-\lambda x}\sin{\lambda x}=-\frac{F\lambda}{2k}B_x\\ M=\frac{F}{4\lambda}e^{-\lambda x}(\cos {\lambda x}-\sin{\lambda x})=\frac{F}{4\lambda}C_x\\ V=-\frac{F}{2}e^{-\lambda x}\cos{\lambda x}=-\frac{F}{2}D_x$$

这里： $$A_x=e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})\\ B_x=e^{-\lambda x}\sin{\lambda x}\\ C_x=e^{-\lambda x}(\cos {\lambda x}-\sin{\lambda x})\\ D_x=e^{-\lambda x}\cos{\lambda x}$$ 下图给出了挠度、转角，弯矩、剪力等的具体图示（这里梁表示有些问题，应理解为无限长）

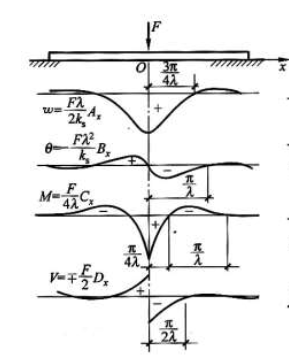
图中可以看到当$x\lambda=3\pi/4$时，挠度为0。更往外，挠度出现负值，表明为拉力。对于实际土体而言，这是不可能出现的。

根据对称性可以得到负半轴结果。

当$x<0$时，根据$w(x)=w(-x)$，可得： $$w=\frac{F\lambda}{2K}e^{\lambda x}(\cos {\lambda x}-\sin{\lambda x})=\frac{F\lambda}{2K}A_{-x}\\ \theta=-\frac{F\lambda }{2k}e^{\lambda x}\sin{\lambda x}=\frac{F\lambda}{2k}B_{-x}\\ M=\frac{F}{4\lambda}e^{\lambda x}(\cos {\lambda x}+\sin{\lambda x})=\frac{F}{4\lambda}C_{-x}\\ V=\frac{F}{2}e^{\lambda x}\cos{\lambda x}=\frac{F}{2}D_{-x}$$

力矩作用

对于顺时针力矩作用，直接引用相关书籍中的结果。

（1）当$x\geq 0$时， $$w=\frac{M_0\lambda^2}{K}e^{-\lambda x}\sin{\lambda x}=\frac{M_0\lambda^2}{K}B_x\\ M=\frac{M_0\lambda}{2}D_x\\ V=-\frac{M_0\lambda}{2}A_x$$

（2）当$x<0$时， $$w=\frac{M_0\lambda^2}{K}e^{-\lambda x}\sin{\lambda x}=\frac{M_0\lambda^2}{K}B_x\\ M=-\frac{M_0\lambda}{2}D_x\\ V=-\frac{M_0\lambda}{2}A_x$$

居中力矩作用下位移、内力等如下图。

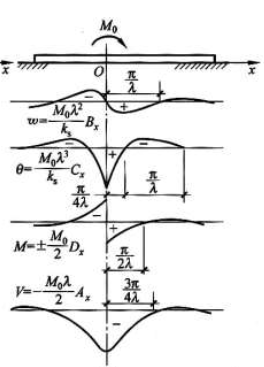
对于上述结果可以列表归纳：

	F，右侧	F，左侧	M，右侧	M，左侧
$w$	$\frac{F\lambda}{2K}A_x$	$\frac{F\lambda}{2K}A_{-x}$	$\frac{M_0\lambda^2}{K}B_x$	$-\frac{M_0\lambda^2}{K}B_{-x}$
$M$	$\frac{F}{4\lambda}C_x$	$\frac{F}{4\lambda}C_{-x}$	$\frac{M_0\lambda}{2}D_x$	$-\frac{M_0\lambda}{2}D_{-x}$
$F$	$-\frac{F}{2}D_x$	$\frac{F}{2}D_{-x}$	$-\frac{M_0\lambda}{2}A_x$	$-\frac{M_0\lambda}{2}A_{-x}$

有限长度居中受集中荷载

实际梁均为有限长度，记长度为$l$。等效于在无限长梁$x=l/2$和$x=-l/2$处作用有反向荷载，使两端部（左端右侧、右端左侧）实际弯矩和剪力为零。

记在右端$x=l/2$施加的反向荷载为$F_1$和$M_1$，在左端$x=-l/2$施加的反向荷载为$F_2$和$M_2$。根据对称性，应有： $$F_1=F_2\\ M_1=-M_2$$

挠度公式

（1）无限长梁$x=0$处作用有集中力$F$时在$x=l/2$处的弯矩和剪力为： $$M_{l/2}=\frac{F}{4\lambda}e^{-\frac{\lambda l}{2}}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})\\ V_{l/2}=-\frac{F}{2}e^{-\frac{\lambda l}{2}}\cos\frac{\lambda l}{2}$$ $x=l/2$处作用有集中力$F_1$时在$x=l/2$左侧处的弯矩和剪力为： $$M_{l/2,F1}=\frac{F_1}{4\lambda}\\ V_{l/2,F1}=\frac{F_1}{2}$$ $x=l/2$处作用有集中力矩$M_1$在$x=l/2$左侧处的弯矩和剪力为： $$M_{l/2,M1}=-\frac{M_1}{2}\\ V_{l/2,M1}=-\frac{M_1\lambda}{2}$$ 类似的可以得到：

$x=-l/2$处作用有集中力$F_2$时在$x=l/2$左侧处的弯矩和剪力为： $$M_{l/2,F2}=\frac{F_2}{4\lambda}C_l\\ V_{l/2,F1}=-\frac{F_2}{2}D_l$$ $x=-l/2$处作用有集中力矩$M_2$在$x=l/2$左侧处的弯矩和剪力为： $$M_{l/2,M1}=\frac{M_2}{2}D_l\\ V_{l/2,M1}=-\frac{M_2\lambda}{2}A_l$$ 根据$x=l/2$处左侧合力为零可以得到： $$M_{l/2}+M_{l/2,F1}+M_{l/2,M1}+M_{l/2,F2}+M_{l/2,M2}=0\\ V_{l/2}+V_{l/2,F1}+V_{l/2,M1}+V_{l/2,F2}+V_{l/2,M2}=0\\ $$ 代入后得： $$M_{l/2}+\frac{F_1}{4\lambda}-\frac{M_1}{2}+\frac{F_2}{4\lambda}C_l+\frac{M_2}{2}D_l=0\\ V_{l/2}+\frac{F_1}{2}-\frac{M_1\lambda}{2}-\frac{F_2}{2}D_l-\frac{M_2\lambda}{2}A_l=0$$ 利用荷载对称性得到： $$M_{l/2}+\frac{F_1}{4\lambda}-\frac{M_1}{2}+\frac{F_1}{4\lambda}C_l-\frac{M_1}{2}D_l=0\\ V_{l/2}+\frac{F_1}{2}-\frac{M_1\lambda}{2}-\frac{F_1}{2}D_l+\frac{M_1\lambda}{2}A_l=0$$ 相应得到： $$M_1=2\alpha_1 V_{l/2}/\lambda-4\beta_1 M_{l/2}\\ F_1=4\alpha_2 V_{l/2}-4\beta_2 M_{l/2}\lambda$$

这里： $$\alpha1=\frac{(1+C_l)}{(1-A_l)(1+C_l)-2(1+D_l)(1-D_l)}\\ \beta1=\frac{(1-D_l)}{(1-A_l)(1+C_l)-2(1+D_l)(1-D_l)}\\ \alpha2=\frac{(1+D_l)}{(1-A_l)(1+C_l)-2(1+D_l)(1-D_l)}\\ \beta2=\frac{(1-A_l)}{(1-A_l)(1+C_l)-2(1+D_l)(1-D_l)}\\ $$

继而有： $$M_2=-2\alpha_1 V_{l/2}/\lambda+4\beta_1 M_{l/2}\\ F_2=4\alpha_2 V_{l/2}-4\beta_2 M_{l/2}\lambda$$

总挠度$w$可以表示为： $$w=w_{F}+w_{M_1}+w_{V_1}+w_{M_1}+w_{V_1}$$ 代入前述计算可得当$x>0时$： $$w=\frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})\\ +\alpha_1\frac{2V_{l/2}\lambda}{K}e^{\lambda (x-l/2)}\sin{\lambda (x-l/2)}\\ -\beta_1\frac{4M_{l/2}\lambda^2}{K}e^{\lambda (x-l/2)}\sin{\lambda (x-l/2)}\\ +\alpha_2\frac{2V_{l/2}\lambda}{K}e^{\lambda (x-l/2)}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\beta_2\frac{2M_{l/2}\lambda^2}{K}e^{\lambda (x-l/2)}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\alpha_1\frac{2V_{l/2}\lambda}{K}e^{-\lambda (x+l/2)}\sin{\lambda (x+l/2)}\\ +\beta_1\frac{4M_{l/2}\lambda^2}{K}e^{-\lambda (x+l/2)}\sin{\lambda (x+l/2)}\\ +\alpha_2\frac{2V_{l/2}\lambda}{K}e^{-\lambda (x+l/2)}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})\\ -\beta_2\frac{2M_{l/2}\lambda^2}{K}e^{-\lambda (x+l/2)}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})$$

代入$M_{l/2}$和$V_{l/2}$可得： $$w=\frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})\\ +\alpha_1\frac{2(-\frac{F}{2}e^{-\frac{\lambda l}{2}}\cos\frac{\lambda l}{2})\lambda}{K}e^{\lambda (x-l/2)}\sin{\lambda (x-l/2)}\\ -\beta_1\frac{4(\frac{F}{4\lambda}e^{-\frac{\lambda l}{2}}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2}))\lambda^2}{K}e^{\lambda (x-l/2)}\sin{\lambda (x-l/2)}\\ +\alpha_2\frac{2(-\frac{F}{2}e^{-\frac{\lambda l}{2}}\cos\frac{\lambda l}{2})\lambda}{K}e^{\lambda (x-l/2)}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\beta_2\frac{2(\frac{F}{4\lambda}e^{-\frac{\lambda l}{2}}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2}))\lambda^2}{K}e^{\lambda (x-l/2)}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\alpha_1\frac{2(-\frac{F}{2}e^{-\frac{\lambda l}{2}}\cos\frac{\lambda l}{2})\lambda}{K}e^{-\lambda (x+l/2)}\sin{\lambda (x+l/2)}\\ +\beta_1\frac{4(\frac{F}{4\lambda}e^{-\frac{\lambda l}{2}}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2}))\lambda^2}{K}e^{-\lambda (x+l/2)}\sin{\lambda (x+l/2)}\\ +\alpha_2\frac{2(-\frac{F}{2}e^{-\frac{\lambda l}{2}}\cos\frac{\lambda l}{2})\lambda}{K}e^{-\lambda (x+l/2)}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})\\ -\beta_2\frac{2(\frac{F}{4\lambda}e^{-\frac{\lambda l}{2}}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2}))\lambda^2}{K}e^{-\lambda (x+l/2)}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})=\\ \frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})\\ -\alpha_1\frac{F\lambda}{K}e^{\lambda (x-l)}\cos\frac{\lambda l}{2}\sin{\lambda (x-l/2)}\\ -\beta_1\frac{F\lambda}{K}e^{\lambda (x-l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})\sin{\lambda (x-l/2)}\\ -\alpha_2\frac{F\lambda}{K}e^{\lambda (x-l)}\cos\frac{\lambda l}{2}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\beta_2\frac{F\lambda}{2K}e^{\lambda (x-l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ +\alpha_1\frac{F\lambda}{K}e^{-\lambda (x+l)}\cos\frac{\lambda l}{2}\sin{\lambda (x+l/2)}\\ +\beta_1\frac{F\lambda}{K}e^{-\lambda (x+l/2)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})\sin{\lambda (x+l/2)}\\ -\alpha_2\frac{F\lambda}{K}e^{-\lambda (x+l)}\cos\frac{\lambda l}{2}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})\\ -\beta_2\frac{F\lambda}{2K}e^{-\lambda (x+l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})$$

梁分类

平均挠度为$F/{Klb}$，则可以得到实际挠度与平均挠度之比： $$w/(F/Kl)=\frac{\lambda l}{2}e^{-\lambda x}(\cos {\lambda x}+\sin{\lambda x})\\ -\alpha_1\lambda le^{\lambda (x-l)}\cos\frac{\lambda l}{2}\sin{\lambda (x-l/2)}\\ -\beta_1\lambda le^{\lambda (x-l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})\sin{\lambda (x-l/2)}\\ -\alpha_2\lambda le^{\lambda (x-l)}\cos\frac{\lambda l}{2}(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ -\beta_2\frac{\lambda l}{2}e^{\lambda (x-l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})(\cos{\lambda (x-l/2)}-\sin{\lambda (x-l/2)})\\ +\alpha_1\lambda le^{-\lambda (x+l)}\cos\frac{\lambda l}{2}\sin{\lambda (x+l/2)}\\ +\beta_1\lambda le^{-\lambda (x+l/2)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})\sin{\lambda (x+l/2)}\\ -\alpha_2\lambda le^{-\lambda (x+l)}\cos\frac{\lambda l}{2}(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})\\ -\beta_2\frac{\lambda l}{2}e^{-\lambda (x+l)}(\cos\frac{\lambda l}{2}-\sin\frac{\lambda l}{2})(\cos{\lambda(x+l/2)}+\sin{\lambda (x+l/2)})$$ 可以看出，对于确定的$\lambda l$，比值取决于$x/l$相关。以下根据不同$\lambda l$进行计算。

（1）$\lambda L=0.001$

x/l	$w_∞$	$w$	$w_M$	$w_V$	挠度比
0	0.500	318.3	-4.10E-07	317.8	100.0%
0.1	0.500	318.3	-3.61E-07	317.8	100.0%
0.2	0.500	318.3	-2.13E-07	317.8	100.0%
0.3	0.500	318.3	3.28E-08	317.8	100.0%
0.4	0.500	318.3	3.77E-07	317.8	100.0%
0.5	0.500	318.3	8.20E-07	317.8	100.0%

这里：

$w_∞$是指无限长情形下的挠度；$w$是指由居中集中力引起的挠度；$w_M$是指由两端弯矩引起的挠度；$w_V$是指由两端集中力引起的挠度。

可以看出，可以视底部反力均匀分布。相应直接可以用均布反力求梁底部的位移。

（2）$\lambda L=\pi/12$

x/l	$w_∞$	$w$	$w_M$	$w_M/w$	$w_V$	$w_V/w$	挠度比
0	0.500	3.820	-0.002	-0.1%	3.322	87.0%	100.0%
0.1	0.500	3.820	-0.002	0.0%	3.322	87.0%	100.0%
0.2	0.499	3.820	-0.001	0.0%	3.322	87.0%	100.0%
0.3	0.497	3.820	0.000	0.0%	3.322	87.0%	100.0%
0.4	0.495	3.820	0.002	0.1%	3.323	87.0%	100.0%
0.5	0.492	3.819	0.004	0.1%	3.323	87.0%	100.0%

（3）$\lambda L=\pi/4$

x/l	$w_∞$	$w$	$w_M$	$w_M/w$	$w_V$	$w_V/w$	挠度比
0	0.500	1.279	-0.009	-0.7%	0.789	61.6%	100.5%
0.1	0.497	1.278	-0.008	-0.6%	0.789	61.8%	100.4%
0.2	0.489	1.276	-0.005	-0.4%	0.792	62.1%	100.2%
0.3	0.476	1.272	0.001	0.1%	0.795	62.5%	99.9%
0.4	0.460	1.268	0.009	0.7%	0.799	63.0%	99.6%
0.5	0.441	1.264	0.019	1.5%	0.804	63.6%	99.3%

（4）$\lambda L=\pi/2$

x/l	$w_∞$	$w$	$w_M$	$w_M/w$	$w_V$	$w_V/w$	挠度比
0	0.500	0.683	-4.94E-18	0.0%	0.183	26.8%	107.3%
0.1	0.489	0.675	-4.36E-18	0.0%	0.186	27.5%	106.0%
0.2	0.460	0.655	-2.59E-18	0.0%	0.194	29.7%	102.8%
0.3	0.420	0.628	3.75E-19	0.0%	0.208	33.1%	98.6%
0.4	0.373	0.598	4.56E-18	0.0%	0.225	37.7%	93.9%
0.5	0.322	0.567	9.98E-18	0.0%	0.245	43.2%	89.1%

（5）$\lambda L=\pi$

x/l	$w_∞$	$w$	$w_M$	$w_M/w$	$w_V$	$w_V/w$	挠度比
0	0.500	0.545	0.045	8.3%	0.00E+00	0.0%	171.3%
0.1	0.460	0.501	0.041	8.1%	5.01E-19	0.0%	157.3%
0.2	0.373	0.399	0.026	6.6%	2.00E-18	0.0%	125.3%
0.3	0.272	0.272	-0.001	-0.2%	4.47E-18	0.0%	85.3%
0.4	0.179	0.136	-0.043	-31.4%	7.79E-18	0.0%	42.9%
0.5	0.104	0.000	-0.104	/	1.17E-17	61.2%	0.0%

（7）$\lambda L=2\pi$

x/l	$w_∞$	$w$	$w_M$	$w_M/w$	$w_V$	$w_V/w$	挠度比
0	0.500	0.497	1.86E-03	0.4%	3.74E-03	0.8%	312.3%
0.1	0.373	0.379	2.55E-03	0.7%	3.64E-03	1.0%	238.0%
0.2	0.179	0.185	3.96E-03	2.1%	2.20E-03	1.2%	116.5%
0.3	0.049	0.049	3.76E-03	7.7%	-3.90E-03	-8.0%	30.5%
0.4	-0.009	-0.030	-2.65E-03	8.7%	-1.88E-02	61.8%	-19.1%
0.5	-0.022	-0.087	-2.16E-02	25.0%	-4.34E-02	50.1%	-54.4%

上述可以看出，

（1）在$\lambda L=\pi$时，端部不产生拉力。

（2）在$\lambda L<\pi/4$，底部挠度接近于相同，因此可以视作均匀反力来进行计算。

在书中的归类是：

根据$\lambda$表达式，下部基础越刚性，越偏向长梁；上部梁越刚性，则偏向于短梁。

至于说倒梁法，其假定底部反力按平衡条件计算，但是其相当于将荷载视为支座，与上述弹性地基梁法的算法是不一样的。从上面可以看出，如果是倒梁法的话，变形只能根据基床系数去求。

刚性梁

对于作用于非中部情形，既然是刚性，又要满足力的平衡，那底部反力只能是倾斜直线分布。

那么这时存在一个问题就是，上部反力引起的反力不能为负，即不能为拉力。

即应有： $$\frac{Ml}{2I}\leq\frac{F}{bl}$$ 相当于： $$\frac{M}{F}\leq \frac{l}{6}$$ 即偏心距不大于$l/6$。否则下部就局部脱空了。

对于偏心距$\xi l/6$时，底部最大应力： $$\frac{\xi l Fl}{12I}+\frac{F}{bl}=(1+\xi)\frac{F}{bl}$$ 理论上应该不能大于基底最大承载力。在偏心距为偏心距$l/6$时，最大反力是轴心受压情形下的两倍。

但是在现行建筑地基基础设计规范中，却是在偏心时将允许的最大承载力放大1.2倍。这样不就有一个问题，我轴心作用不满足，适当偏个非常小的心，如1/10，那反而可能能满足要求。

有限长度任意部位受集中荷载

对于更一般性的情况，这里考虑有线长度梁在任意部位施加集中荷载的情形。

$x=0$处作用有集中力$F$时在$x=l_1$左侧的弯矩和剪力为： $$M_{l_1,F}=\frac{F}{4\lambda}C_{l_1}\\ V_{l_1,F}=-\frac{F}{2}D_{l_1}$$ $x=0$处作用有集中力$F$时在$x=l_2$右侧的弯矩和剪力为： $$M_{l_2,F}=\frac{F}{4\lambda}C_{-l_2}\\ V_{l_2,F}=\frac{F}{2}D_{-l_2}$$ $x=l_1$处作用有集中力$F_1$时在$x=l_1$左侧的弯矩和剪力为： $$M_{l_1,F1}=\frac{F_1}{4\lambda}\\ V_{l_1,F1}=\frac{F_1}{2}$$ $x=l_1$处作用有集中力矩$M_1$在$x=l_1$左侧处的弯矩和剪力为： $$M_{l_1,M1}=-\frac{M_1}{2}\\ V_{l_1,M1}=-\frac{M_1\lambda}{2}$$ $x=l_1$处作用有集中力$F_1$时在$x=l_2$右侧处的弯矩和剪力为： $$M_{l_2,F1}=\frac{F_1}{4\lambda}C_{l}\\ V_{l_2,F1}=\frac{F_1}{2}D_{l}$$ $x=l_1$处作用有集中力矩$M_1$在$x=l_2$右侧处的弯矩和剪力为： $$M_{l_2,M1}=-\frac{M_1}{2}D_{l}\\ V_{l_2,M1}=-\frac{M_1\lambda}{2}A_{l}$$ $x=l_2$处作用有集中力$F_2$时在$x=l_1$左侧处的弯矩和剪力为： $$M_{l_1,F2}=\frac{F_2}{4\lambda}C_{l}\\ V_{l_1,F2}=-\frac{F_2}{2}D_{l}$$ $x=l_2$处作用有集中力矩$M_2$在$x=l_1$左侧处的弯矩和剪力为： $$M_{l_1,M2}=\frac{M_2}{2}D_{l}\\ V_{l_1,M2}=-\frac{M_2\lambda}{2}A_{l}$$ $x=l_2$处作用有集中力$F_2$时在$x=l_2$右侧处的弯矩和剪力为： $$M_{l_2,F2}=\frac{F_2}{4\lambda}\\ V_{l_2,F2}=-\frac{F_2}{2}$$ $x=l_2$处作用有集中力矩$M_2$在$x=l_2$右侧处的弯矩和剪力为： $$M_{l_2,M2}=\frac{M_2}{2}\\ V_{l_2,M2}=-\frac{M_2\lambda}{2}$$ 根据$x=l_1$左侧和$x=l_2$左侧合力为零可以得到： $$M_{l_1,F}+M_{l_1,F1}+M_{l_1,M1}+M_{l_1,F2}+M_{l_1,M2}=0\\ V_{l_1,F}+V_{l_1,F1}+V_{l_1,M1}+V_{l_1,F2}+V_{l_1,M2}=0\\ M_{-l_2,F}+M_{l_2,F1}+M_{l_2,M1}+M_{l_2,F2}+M_{l_2,M2}=0\\ V_{-l_2,F}+V_{l_2,F1}+V_{l_2,M1}+V_{l_2,F2}+V_{l_2,M2}=0$$ 代入后得： $$\frac{F}{4\lambda}C_{l_1}+\frac{F_1}{4\lambda}-\frac{M_1}{2}+\frac{F_2}{4\lambda}C_{l}+\frac{M_2}{2}D_{l}=0\\ -\frac{F}{2}D_{l_1}+\frac{F_1}{2}-\frac{M_1\lambda}{2}-\frac{F_2}{2}D_{l}-\frac{M_2\lambda}{2}A_{l}=0\\ \frac{F}{4\lambda}C_{-l_2}+\frac{F_1}{4\lambda}C_{l}-\frac{M_1}{2}D_{l}+\frac{F_2}{4\lambda}+\frac{M_2}{2}=0\\ \frac{F}{2}D_{-l_2}+\frac{F_1}{2}D_{l}-\frac{M_1\lambda}{2}A_{l}-\frac{F_2}{2}-\frac{M_2\lambda}{2}=0$$ 或依旧可表示为： $$M_{l_1,F}+\frac{F_1}{4\lambda}-\frac{M_1}{2}+\frac{F_2}{4\lambda}C_{l}+\frac{M_2}{2}D_{l}=0\\ V_{l_1,F}+\frac{F_1}{2}-\frac{M_1\lambda}{2}-\frac{F_2}{2}D_{l}-\frac{M_2\lambda}{2}A_{l}=0\\ M_{-l_2,F}+\frac{F_1}{4\lambda}C_{l}-\frac{M_1}{2}D_{l}+\frac{F_2}{4\lambda}+\frac{M_2}{2}=0\\ V_{-l_2,F}+\frac{F_1}{2}D_{l}-\frac{M_1\lambda}{2}A_{l}-\frac{F_2}{2}-\frac{M_2\lambda}{2}=0$$

对于上述方程租，可以进行求解。

4个未知数：$F_1,M_1,F_2,M_2$

解得： $$F_1=\frac{M_{l1,F}(4{A_l}^2- 8{D_l}^2+ 4)\lambda +M_{-l2,F}(-4{A_l}^2C_l + 8A_l{D_l}^2 - 8A_l + 4C_l)\lambda +V_{l1,F}(-4A_lC_l + 4A_lD_l- 4C_lD_l + 8{D_l}^2 - 4) +V_{-l2,F}(4A_lC_lD_l - 4A_l + 4C_l - 8{D_l}^3 + 4D_l)}{(A_lC_l- 2{D_l}^2 + 1 + A_l-C_l)(A_lC_l - 2{D_l}^2 + 1- A_l+C_l)}$$

$$M_1=\frac{M_{l1,F}(4A_lC_l+4A_lD_l-4C_lD_l-8{D_l}^2+ 4)\lambda +M_{-l2,F}(-4A_lC_l D_l-4A_l+4C_l + 8{D_l}^3 - 4D_l)\lambda +V_{l1,F}(-2{C_l}^2+4{D_l}^2-2) +V_{-l2,F}(2A_l{C_l}^2 - 2A_l -4C_l{D_l}^2 + 4C_l)}{(A_lC_l- 2{D_l}^2 + 1 + A_l-C_l)(A_lC_l - 2{D_l}^2 + 1- A_l+C_l)\lambda }$$

$$F_2=\frac{M_{l1,F}(-4{A_l}^2C_l +8A_l{D_l}^2 - 8A_l + 4C_l)\lambda+M_{-l2,F}(4{A_l}^2-8{D_l}^2+ 4)\lambda +V_{l1,F}(-4A_lC_lD_l +4A_l -4C_l +8{D_l}^3 - 4D_l)+V_{-l2,F}(4A_lC_l - 4A_lD_l+ 4C_lD_l -8{D_l}^2 + 4) }{(A_lC_l- 2{D_l}^2 + 1 + A_l-C_l)(A_lC_l - 2{D_l}^2 + 1- A_l+C_l)}$$

$$M_2=\frac{ -M_{l1,F}(-4A_lC_l D_l-4A_l+4C_l + 8{D_l}^3 - 4D_l)\lambda+M_{-l2,F}(4A_lC_l+4A_lD_l-4C_lD_l-8{D_l}^2+ 4)\lambda +V_{l1,F}(2A_l{C_l}^2 - 2A_l -4C_l{D_l}^2 + 4C_l)+V_{-l2,F}(-2{C_l}^2+4{D_l}^2-2) }{(A_lC_l- 2{D_l}^2 + 1 + A_l-C_l)(A_lC_l - 2{D_l}^2 + 1- A_l+C_l)\lambda }$$

当荷载作用于居中位置时， $$C_{l1}=C_{l2}\\ D_{l1}=D_{l2}\\ $$ 代入后得： $$\frac{F}{4\lambda}C_{l_1}+\frac{F_1}{4\lambda}-\frac{M_1}{2}+\frac{F_2}{4\lambda}C_{l}+\frac{M_2}{2}D_{l}=0\\ -\frac{F}{2}D_{l_1}+\frac{F_1}{2}-\frac{M_1\lambda}{2}-\frac{F_2}{2}D_{l}-\frac{M_2\lambda}{2}A_{l}=0\\ \frac{F}{4\lambda}C_{l_1}+\frac{F_1}{4\lambda}C_{l}-\frac{M_1}{2}D_{l}+\frac{F_2}{4\lambda}+\frac{M_2}{2}=0\\ \frac{F}{2}D_{l_1}+\frac{F_1}{2}D_{l}-\frac{M_1\lambda}{2}A_{l}-\frac{F_2}{2}-\frac{M_2\lambda}{2}=0$$ 此时与前述解一致。

总挠度$w$可以表示为： $$w=w_{F}+w_{M_1}+w_{V_1}+w_{M_1}+w_{V_1}$$ 代入前述计算可得挠度公式为： $$w=\frac{F\lambda}{2K}e^{-\lambda x}(\cos {\lambda x}+\sin {\lambda x})+\\ \frac{F_1\lambda}{2K}e^{-\lambda (l_1-x)}(\cos {\lambda (l_1-x)}+\sin {\lambda (l_1-x)})+\\ -\frac{M_1(\lambda)^2}{K}e^{-\lambda (l_1-x)}(\sin {\lambda (l_1-x)})+\\ \frac{F_2\lambda}{2K}e^{-\lambda (x-l_2)}(\cos {\lambda (x-l_2)}+\sin {\lambda (x-l_2)}+\\ \frac{M_1(\lambda)^2}{K}e^{-\lambda (x-l_2)}(\sin {\lambda (x-l_2)})$$

这里直接采用程序进行计算。

不考虑受拉区域

前面可知，当荷载居中作用时，当$\lambda l=\pi$时，恰不出现受拉区，荷载右侧受压区长度是左侧1倍。伴随荷载偏离，对于$l_2\leq x\leq -l_2$区域，此时对于此段$\lambda l<\pi$，故此区域应全部受压。而当$|l_2|$不断减小，即荷载靠近一端时，$\lambda l$趋向于0，此时受压区应为对于$l_2\leq x\leq -2l_2$区域，荷载右侧受压区长度是左侧2倍。

记左侧长度与总长比为$\gamma$,右侧受压区长度与左侧长度比为$\zeta$，可以计算得到如下图所示数据。

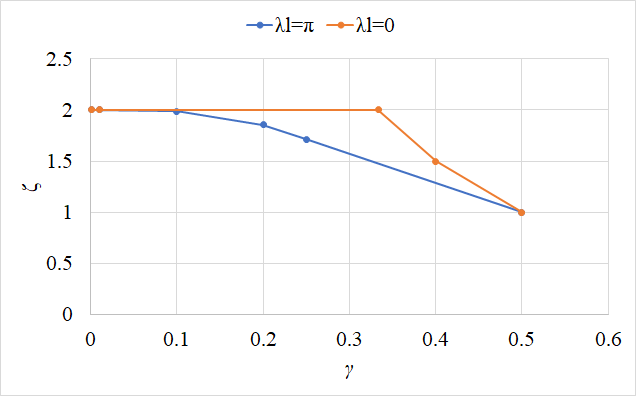
进一步的可以得到底部最大应力与平均值之比，当荷载与左端距离趋向于零时，比值趋向于无穷大。

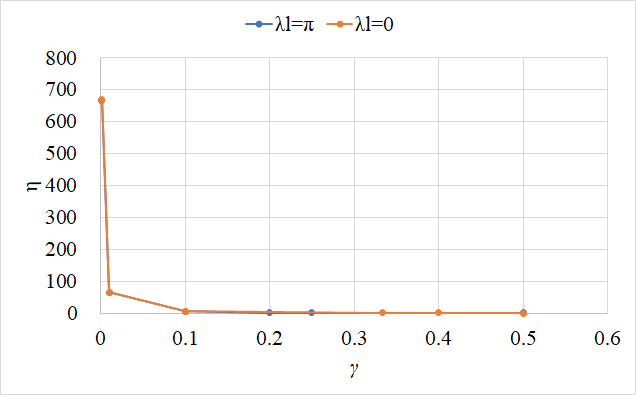
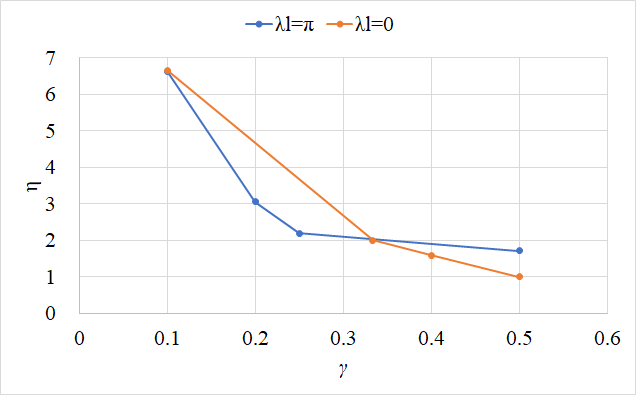
（1）当在一端时，$\gamma\le 0.1$时，由于是非常短梁，基床系数的影响就很小了。此时扩散效应也很小，因此应尽可能避免；

（2）在下述$0.1\leq \gamma\leq 0.33$区域，基床系数越大，底部最大应力越小；

（3）$0.33\le \gamma$时，基床系数越大，底部最大应力就越大。

所以实际上无法统一认为下部土体那种对于扩散应力更有利，需要结合荷载作用部位。

---

最后更新：2025年10月10日 星期五 天气晴