桁架
首先需要明确对象关系。对象类名及方法均采用大驼峰式命名,属性均为小驼峰,以区别于通常的python中的小写命名方式。最顶层对象类似于Abaqus中的顶层mdb对象,其有且只有一个。我们将其视为my_truss模块顶层对象:Truss2D:理论上可以建立多个Truss2D对象用以比较分析 次级对象:均由Truss2D对象生成Result:结果文件对象Bar2D:2……
抗规中对于框架-剪力墙结构中基于底层框架倾覆力矩占总倾覆力矩的比值进行分类设计。并在条文说明中给出了计算底层框架倾覆力矩的公式,但这个公式是否合理?本文给出相关推导并进行适当讨论……
在这篇文章里地震倾覆力矩的计算 - 道客巴巴将倾覆力矩这个问题也是讲的比较清楚。这里自行再推导下。
对于基底弯矩,可以表示为: 这里:
——第层水平荷载;——第层高度。
记为第层层高,则: 相应有: 上式右端求和项中
当时: 当时: 当时: 则: 这里: 为第层的总剪力。
故:
记为第层第号竖向构件的剪力,则有式(1):
相应的,可以将其分为柱部分,墙部分:
这里为柱数目,为墙数目。
可以看到上述表达式与抗规6.1.3条中条文说明的公式相同。不过上面的只是一种定义,其物理意义呢。这里的是否能代表底层柱实际承受的倾覆力矩呢?
理论上对于基底弯矩可以另外表达成: 这里:
、——底层第号构件轴力、弯矩;——底层第号构件与轴心的距离。
相应的底层柱承受的倾覆力矩可以表示为:
对于一些情形,上述倾覆力矩还有另一种表达方式。若各号柱通高,记第层第号所受水平、竖向荷载及弯矩为,,。则:
则有式(2):
这里:
这里:
利用第1节中的推导可得:
相应有式(3):
可以看到,只有当满足式(4)
有:
注:在上述讨论中,对于力的正负号不做规定。实际计算时有必要明确。
显然由上述推导可以得到,对于纯框架结构而言,应有式(4)一定成立。例如对于两榀框架结构,满足:
相应也易证明满足式(4)。但是这不代表式(4)一定是成立的。也就是说,抗规中所谓的底层倾覆力矩表达式并不代表实际的倾覆力矩的大小。而在PKPM WV02Q文件中,如下图所示,也保留着两者的对比。
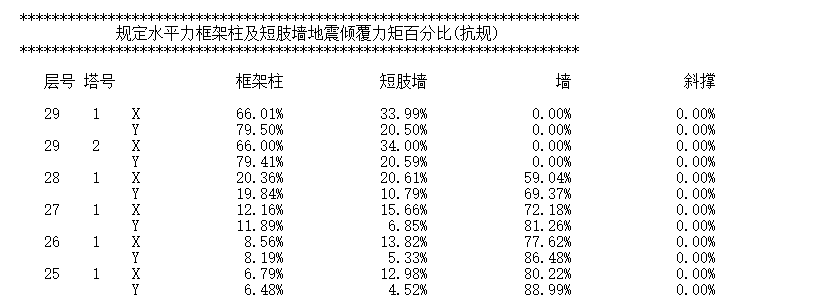
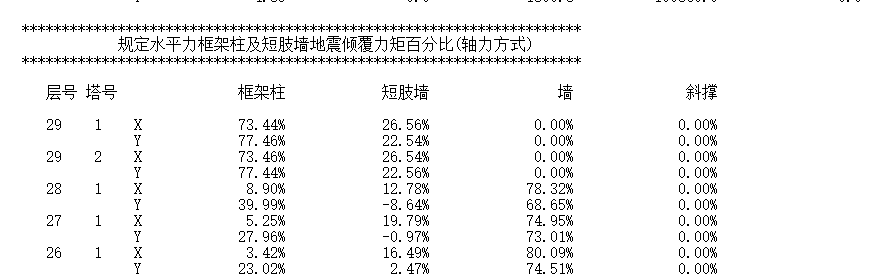
值得注意的是,各种构件的倾覆力矩的百分比并不是都为正的。这也就是说实际有可能出现一种100%多,而另一种为负的情形。
不过无论规范中所给底层倾覆力矩是否与精确解接近,有一个比较关键的问题是,为什么能用倾覆力矩来区别设计不同类型的框架-剪力墙结构。
高钢规8.1.3条条文说明中只是提到:
框架-剪力墙结构在规定的水平力作用下,结构底层框架部分承受的地震倾覆力矩与结构总地震倾覆力矩的比值不尽相同,结构性能有较大的差别。
似乎这也是一个可以探讨的问题。
注:上述推导中运用了双重求和∑∑的定义及性质