1、为什么选择开始采用平面桁架进行编程

主要原因在单元刚度矩阵相对简单，与此同时边界条件也简单。不需要考虑积分方式和等参元等。

2、对象关系架构

首先需要明确对象关系。对象类名及方法均采用大驼峰式命名，属性均为小驼峰，以区别于通常的python中的小写命名方式。

最顶层对象

类似于Abaqus中的顶层mdb对象，我们将其视为my_truss模块

顶层对象：

Truss2D：理论上可以建立多个Truss2D对象用以比较分析

次级对象：均由Truss2D对象生成

Result：结果文件对象

Bar2D：2维杆单元

Node：节点对象

模块

模块变量： trusses 用于存储所有Truss2D实例

生成Truss2D对象后，基于该对象生成节点、杆件等。相关命令参考CAD ActiveX，相关方法均以Add打头。

Truss2D类

class Truss2D():
    def __init__(self,name):
        self.__name = name
        self.__bars= []
        self.__nodes = []
        self.__numNode = 0        
        trusses[name] = self # 在trusses字典中增加该对象，用于索引

    # 添加节点
    def AddNode(self,n,x1,y1):
        p = Node(n,x1,y1)  # 生成节点对象
        self.nodes.append(p)
        self.numNode += 1
        return p

    # 以两节点编号确定单元
    def AddBar(self,n1,n2):
        aa = Bar2D(self,n1,n2) # 生成Bar2D对象
        self.bars.append(aa)
        return aa

理论上上述生成对象的方法都是可以不带参数的，然后对于各个对象采用自身类中的定义确定其属性。

该对象相关属性和方法

属性	含义	方法	含义
bars	杆件列表（R)	AddNode	以节点坐标添加节点
nodes	节点列表（R)	AddBar	以两节点编号添加杆件
numNode	节点数（R)
name	项目名称（R）
K	整体刚度矩阵（R)	Solve	求解
forceVec	荷载向量（R）	Check	检查输入正确性
dispVec	位移向量（R）

定义节点类

# 定义节点类
class Node():
    def __init__(self,n,x,y):
        self.__nodeN  = n
        self.x = x
        self.y = y
        self.DispX = 'U-defined'
        self.DispY = 'U-defined'
        self.FX = 0
        self.FY = 0

    @property
    def nodeN(self):
        return self.__nodeN

对于节点而言，相关属性和方法有：

属性	含义	方法	含义
nodeN	节点号（R)
x	节点整体坐标系下X坐标（W/R)
y	节点坐标系下Y坐标（W/R)
dispX	节点坐标系下X向位移（W/R)
dispY	节点坐标系下Y向位移（W/R)

定义Bar2D类

# 定义杆件对象
# 默认截面面积 100
# 默认弹性模量2.0e5 
class Bar2D():
def __init__(self,truss,n1,n2,area = 100,Es = 2.0e5):
    self.node1 = n1
    self.node2 = n2
    point1 = truss.nodes[n1-1]
    point2 = truss.nodes[n2-1]
    self.p1 = (point1.x,point1.y)
    self.p2 = (point2.x,point2.y)
    self.E = Es
    self.A = area
    self.delta_y = self.p2[1]-self.p1[1]
    self.delta_x = self.p2[0]-self.p1[0]

属性	含义	数据
KE	整体坐标系下单元刚度矩阵（R)	ndarray
KE0	局部坐标系下单元刚度矩阵（R)	ndarray
GE	转换矩阵（R)	ndarray
length	长度（R）	数值
A	面积 (R/W)	数值
E	弹性模量（R/W）	数值

Result类

属性	含义	数据
axisForces	杆件轴力（R）	list
nodeDisps	节点位移（R）	list
nodeForces	节点反力（R）	llist

3、涉及到矩阵运算

采用numpy模块

需要numpy

https://www.numpy.org.cn/

https://www.numpy.org/devdocs/user/quickstart.html#array-creation

转置矩阵

集成整体刚度矩阵

根据位移边界条件简化（缩聚）

计算向量值

得到节点位移

然后得到杆件内力，应力等等

后处理会涉及到图形绘制等问题

暂时不会涉及到等参单元高斯积分等问题

这其中本专业比较重要的其实是单元刚度矩阵如何推导的问题。

其他的都并不是我们所擅长的方面了。

有一个问题是使用类属性还是特性的问题

目标:先计算得到结构力学书中的解答

基本上算是大功告成，算出的内力结果完全一致

numpy.delete()

不过还有几个问题：

如何判断输入的结构是否正确，报错功能

再编写一个输入界面

还需要绘制输出文件

3、模块完整代码

# 计算桁架库
# 2019年6月29日 星期六 天气晴热
# 版权所有©-Y-__-Y-
# wwww.kiritanimirei.cn
# 2019年8月22日 星期四 天气晴
# 2019年8月19日 星期一 天气晴

import math
import numpy as np

# 模块变量
trusses = {}

# 定义节点类
class Node():
    def __init__(self,n,x,y):
        self.__nodeN = n
        self.x = x
        self.y = y
        self.dispX = 'U'
        self.dispY = 'U'
        self.FX = 0
        self.FY = 0

    @property
    def nodeN(self):
        return self.__nodeN

    # 设置位移
    def DispNode(self,x,y):
        self.dispX = x
        self.dispY = y
        # 修改整体位移向量

    # 设置荷载
    def FNode(self,fx,fy):
        self.FX = fx
        self.FY = fy
        # 修改整体荷载向量


# 定义杆件对象
# 默认截面面积 100
# 默认弹性模量2.0e5   
class Bar2D():

    def __init__(self,truss,n1,n2,area = 100,Es = 2.0e5):
        self.node1 = n1
        self.node2 = n2
        point1 = truss.nodes[n1-1]
        point2 = truss.nodes[n2-1]
        self.p1 = (point1.x,point1.y)
        self.p2 = (point2.x,point2.y)
        self.E = Es
        self.A = area
        self.delta_y = self.p2[1]-self.p1[1]
        self.delta_x = self.p2[0]-self.p1[0]



    # 使用特性
    @property
    def length(self):
        # 用于得到杆件长度
        return math.sqrt(self.delta_y*self.delta_y+self.delta_x*self.delta_x)

    # 转换矩阵
    @property
    def GE(self):

        cos_t = self.delta_x/ self.length
        sin_t = self.delta_y/ self.length
        aa = np.zeros((2,2 ))
        bb = np.zeros((2, 2))
        aa[0,0] = cos_t
        aa[0,1] = sin_t
        aa[1,0] = -sin_t
        aa[1,1] = cos_t

        cc=np.concatenate((aa ,bb), axis=1)
        dd=np.concatenate((bb ,aa), axis=1)
        GMat =np.zeros((2,4))
        GMat[0,0]=cos_t
        GMat[0,1]=sin_t
        GMat[1,2]=cos_t
        GMat[1,3]=sin_t

        return GMat

    # 获取整体坐标系下单元刚度矩阵
    @property
    def KE(self):
        KMat = np.dot(self.GE.T,self.KE0)
        KMat = np.dot(KMat,self.GE) 
        return KMat

    # 获取局部坐标系下单元刚度矩阵
    @property
    def KE0(self):
        KMat = np.array([[1,-1],[-1,1]])
        KMat = KMat*self.A*self.E/self.length        
        return KMat



class Result():
    def __init__(self,u,f,bars):
        self.__U = u
        self.__F = f
        self.bars = bars

    def FE(self,nb):
        k = self.bars[nb-1].KE0
        g= self.bars[nb-1].GE
        n1 = self.bars[nb-1].node1
        n2 = self.bars[nb-1].node2
        aa = [2*(n1-1),2*(n1-1)+1,2*(n2-1),2*(n2-1)+1]
        u1 = self.__U[aa]
        u1_e = np.dot(g,u1)
        f1_e = np.dot(k,u1_e) 
        return round(f1_e[1],3)

    # 得到各杆件内力
    @property
    def axisForces(self):
        num = len(self.bars)
        NVec = [self.FE(i+1) for i in range(num)]
        return NVec

    # 得到各节点位移
    @property
    def nodeDisps(self):
        return self.__U

    # 得到各节点荷载（包括支座反力）
    @property
    def nodeForces(self):
        return self.__F


# 顶层类，对于每一个
class Truss2D():
    def __init__(self,name):
        self.__name = name
        self.__bars= []
        self.__nodes = []
        self.__numNode = 0        
        trusses[name] = self # 在trusses字典中增加该对象，用于索引

    @property
    def name(self):
        return self.__name

    @property
    def bars(self):
        return self.__bars

    @property
    def nodes(self):
        return self.__nodes

    @property
    def numNode(self):
        return self.__numNode

    # 以两节点编号确定单元
    # n1,n2 节点1编号，节点2编号
    def AddBar(self,n1,n2):
        aa = Bar2D(self,n1,n2)
        self.__bars.append(aa)
        return aa

    # 添加节点
    # n,x1,y1 节点编号，x坐标，y坐标
    def AddNode(self,n,x1,y1):
        p = Node(n,x1,y1)
        self.__nodes.append(p)
        self.__numNode += 1
        return p

    # 添加荷载约束
    def AddF(self,n1,fx,fy):
        point1 = self.nodes[n1-1]
        point1.FX = fx
        point1.FY = fy

    # 添加位移约束
    def AddDisp(self,n1,d1,d2):
        point1 = self.nodes[n1-1]
        point1.dispX = d1
        point1.dispY = d2


    # 求解
    def Solve(self):
        aa = len(self.bars)
        FVec = self.forceVec
        DVec = self.dispVec
        ee = list(np.where(DVec!='0')[0])
        FVec2 = FVec[ee] # 得到缩聚后的荷载向量

        # 获得缩聚后的刚度矩阵         
        KMat = self.K
        K1 = KMat[ee]   
        K2 = K1[:,ee]

        u0 = np.linalg.solve(K2, FVec2)        
        U = np.zeros((self.numNode*2))
        U[ee] = u0
        F = np.dot(self.K,U)
        out = Result(U,F,self.bars)

        # 输出相关信息
        print("求解完毕")
        return out




    # 得到荷载向量
    @property
    def forceVec(self):
        aa = []
        for obj in self.nodes:
            aa.append(obj.FX)
            aa.append(obj.FY)
        return np.array(aa)

    # 得到位移向量
    @property
    def dispVec(self):
        aa = []
        for obj in self.nodes:
            aa.append(obj.dispX)
            aa.append(obj.dispY)
        return np.array(aa)

    # 得到整体刚度矩阵
    @property
    def K(self):
        aa = len(self.bars)
        KMat = np.zeros((self.numNode*2,self.numNode*2))
        for i in range(aa):
            bar = self.bars[i]
            ke = bar.KE
            n1 = bar.node1
            n2 = bar.node2
            # print(ke[2:4,2:4])
            KMat[2*(n1-1):2*(n1-1)+2,2*(n1-1):2*(n1-1)+2] += ke[0:2,0:2]
            KMat[2*(n1-1):2*(n1-1)+2,2*(n2-1):2*(n2-1)+2] += ke[0:2,2:4]
            KMat[2*(n2-1):2*(n2-1)+2,2*(n1-1):2*(n1-1)+2] += ke[2:4,0:2]
            KMat[2*(n2-1):2*(n2-1)+2,2*(n2-1):2*(n2-1)+2] += ke[2:4,2:4]
        return KMat

案例计算

角钢桁架

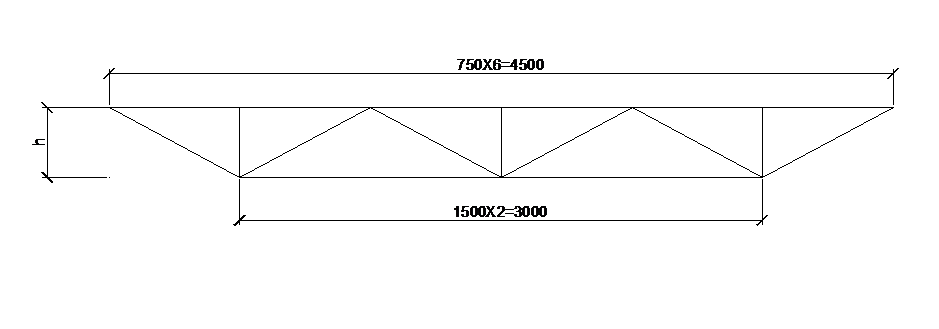
# 本程序用于计算一矩形桁架
# 2019年8月16日 星期五 天气晴
# 版权所有©-Y-__-Y-
# wwww.kiritanimirei.cn
# python风格代码

# 2019年8月19日 星期一 天气雷阵雨 

from my_truss import Truss2D,trusses


# 设置参数
num = 6 # 上弦杆分段数 上、下弦杆节点数目num+1,num/2

l = 4500 # 跨度
d = l/num # 上弦杆杆长
h = 500 #矢高
bar_num = int(num + (num-2)/2 + 3 * num/2) # 总杆件数目


# 建立新的模型
truss1 = Truss2D('my_truss')

# 添加节点
x_li = [i*d for i in range(num+1)] + [d +2*i*d for i in range(int(num/2))]
y_li = [0 for i in range(num+1)] + [-1*h for i in range(int(num/2))]

[truss1.AddNode(i+1,x_li[i],y_li[i]) for i in range(int(3*num/2+1))]

# 添加杆件单元

# 依次添加上弦杆、下弦杆、斜腹杆1、斜腹杆2和竖腹杆
bar_li1 = [i+1 for i in range(num)] + \
   [i+num+2 for i in range(int(num/2-1))] + \
   [i*2+1 for i in range(int(num/2))] + \
   [i+num+2 for i in range(int(num/2))]+ \
   [2*i+2 for i in range(int(num/2))] 
bar_li2 = [i+2 for i in range(num)] + \
   [i+num+3 for i in range(int(num/2-1))] + \
   [i+num+2 for i in range(int(num/2))] + \
   [i*2+3 for i in range(int(num/2))]+ \
   [i+num+2 for i in range(int(num/2))]    
bar_li = [bar_li1,bar_li2] 


# 建立杆件
for i in range(bar_num):
    truss1.AddBar(bar_li[0][i],bar_li[1][i])

# 赋予面积               
area_li = [498 for i in range(num)] + [439 for i in range(int(num/2-1))] + \
          [349 for i in range(num)] + [349 for i in range(int(num/2))] 
for i, obj in enumerate(truss1.bars):
   obj.A = area_li[i]+10




# 添加边界条件    
truss1.AddF(1,0,-3940)
for i in range(num-1):
   truss1.AddF(i+2,0,-7880)                                       
truss1.AddF(num+1,0,-3940)

truss1.AddDisp(1,0,0)
truss1.AddDisp(num+1,'U',0)


# 求解
Out = truss1.Solve()


##  后处理
# 得到各杆件内力和位移
NVec = Out.axisForces # 所有杆件内力

桁架

2020年02月12日星期三

1、为什么选择开始采用平面桁架进行编程

2、对象关系架构

模块

Truss2D类

定义节点类

定义Bar2D类

Result类

3、模块完整代码

案例计算

精选博客

博士论文致谢

2-对象结构与数据类型

终于考完了

桁架

2020年02月12日 星期三

1、为什么选择开始采用平面桁架进行编程

2、对象关系架构

模块

Truss2D类

定义节点类

定义Bar2D类

Result类

3、模块完整代码

案例计算

精选博客

博士论文致谢

2-对象结构与数据类型

终于考完了

2020年02月12日星期三