岳阳会议小记
领导让去湖南岳阳参加一个标准启动会议。先说说怎么去的岳阳。杭州到岳阳没有直达火车或是飞机,基本上只能通过长沙中转过去。杭州到长沙有一个杭长客运专线,单程时长大概最快4小时略微不到,长的需要4小时45分左右(相对于去武汉还是会快一些)。沿途经过金华、衢州、上饶、南昌等,也就是说走的是浙江——江西——湖南这条线。而长沙纬度比杭州还低(北纬27°51′~28°41′之间,而杭州大致在30°上下)。……
在应用变分原理后有限元问题最后会转化对泛函的求导。本文将讲解对于泛函中被积函数具有二次项形式时所得到方程的形式。
为了后续推导,需要有下述数学公式。(相关公式可以网上搜索得到)
二次型关于向量求导:
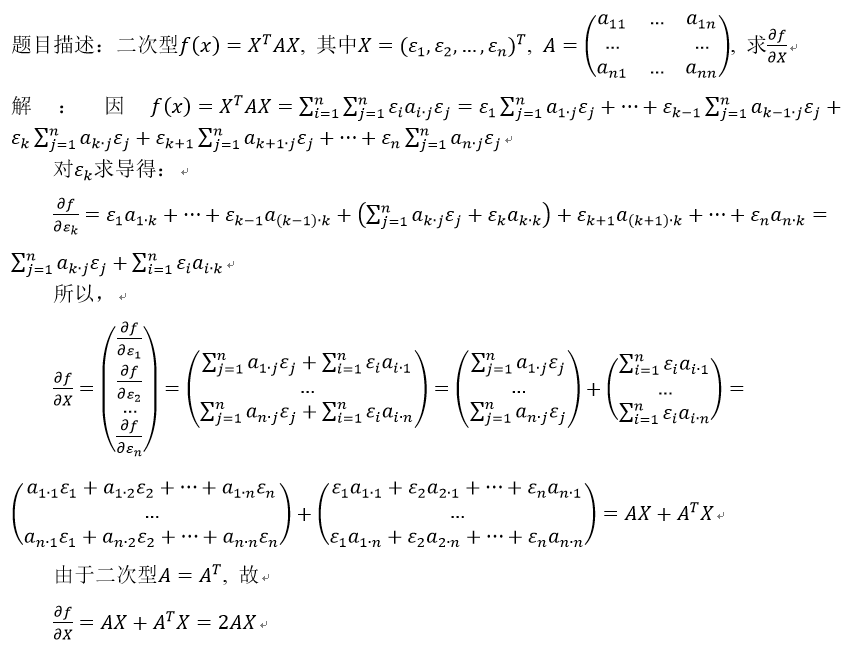
标量和对向量求导的公式: 向量积对标量求导公式:
采用变分原理时,如果泛函积分项中被积函数为关于整体位移 及其导数的二次函数,即
对求导可应用标量和对向量求导的公式: 故这里首先推导上述二次型中第一项的导数。
1)整体坐标系下
上述可以表示为 在整体坐标系下,与的关系式为: 故进一步可表示为: 这里为节点转换矩阵。
此时可表示为: 相对于的导数按照二次项导数公式为: 相应的可记上述积分项为整体坐标系下单元刚度矩阵为: 整体刚度矩阵: 可以看出,若是对称的,则整体刚度也应是对称的。
2)局部坐标系
一般积分都是在局部坐标系进行的,此时上述均应是在局部坐标系下,后续推导过程一致,不过与的关系式应为: 对于可参看相关对于坐标转换的讲解。
此时相应可得到相对于的导数按照二次项导数公式为: 记局部坐标系下单元刚度矩阵为: 相应的可以看到此时在集成整体坐标系过程中,需要做两步:
①坐标转换,②节点转换
3)导数部分
对于二次型的一次导数部分,利用向量积对标量求导公式: 有: 相应的可知局部坐标系下单元刚度矩阵为: 对于n阶导数类似可以总结为: 4)节点荷载
一次项类似的可表示为在局部坐标系下: 相应可以得到单元等效节点荷载为:
整体等效节点荷载: 综上,得到有限元方程: 对于原本荷载就施加在节点上的情形,其在泛函中可表达为: 其对于导数为。
对于平面杆系结构而言,可建立平面直角坐标系。记局部坐标系下杆件沿轴向位移为,沿法向为,势能在可表示为: 注意到实际上上述势能项是局部坐标和整体坐标的混搭,而积分项是在基于杆件的局部坐标系下推导得到的。
若记: 则第一项内力势能被积函数可以表示成二次项为: 其中: 形函数取: 则局部坐标系下单元刚度矩阵为:
要应用Python在CAD中需要两方面的知识,一是ActiveX Automation,这个是AutoCad中基础二次开发接口。ActiveX Automation标准是微软公司基于COM(组件对象模型)体系结构开发的一项技术,允许用户由一个Windows应用程序控制另一个Windows应用程序,实现数据共享,代替重复性的手工操作。用户可以选择合适的编程语言实现此功能,CAD中推荐采用的VBA(V……