关于三级连接对接焊缝不用验算问题
在《钢结构连接节点设计手册》中，对于对接接头的全熔透焊缝，提到如果轴力与焊缝夹角满足tanθ≤1.5\tan\theta\leq 1.5，则采用三级焊缝也满足要求。但书里并没有提到这一点。……
讲一个很少或几乎没有书去讲的一个问题，就是关于如何解读荷载-位移曲线的。判断平衡状态是否稳定可通过应用Ляпунов（李雅普诺夫）一次近似理论[1]，即对于方程通过特征值实部正负来加以判断： （1）如果其特征方程所有特征根均具负实部，则进行轻微扰动后，将依旧回到原平衡位置； （2）如果特征方程至少具有一个正实部的根，则进行轻微扰动后，将无法回复到原平衡位置。……
讲一个很少或几乎没有书去讲的一个问题，就是关于如何解读荷载-位移曲线的。荷载-位移曲线的每一个点相当于一个平衡位置，对于每一个平衡位置，存在运动微分方程： 上述微分方程特征值为： 判断平衡状态是否稳定可通过应用Ляпунов（李雅普诺夫）一次近似理论[1]，即对于方程通过特征值实部正负来加以判断：
（1）如果其特征方程所有特征根均具负实部，则进行轻微扰动后，将依旧回到原平衡位置；
（2）如果特征方程至少具有一个正实部的根，则进行轻微扰动后，将无法回复到原平衡位置。
一般的认为系统具有正阻尼，即阻尼系数：
当时，即刚度为负时，特征根为实数，且具有为正实部，平衡位置不稳定。
当时，即刚度为负时，特征根为实数，且具有一个0值，此时平衡状态不确定。
当时，即刚度为正时，特征根为实数，且实部均小于0，此时平衡位置稳定。
当时，特征根为虚数，实部为，此时平衡位置稳定。
需要注意的是上述稳定都是相对于平衡位置的，刚度相当于切线刚度。综上可知，判断平衡位置稳定与否取决于切线刚度正负。所以就会有极值点失稳（如下图所示）这一说法，在极值点之后，虽然依旧有平衡状态，但是不稳定的，实际相当于不能再承受荷载。
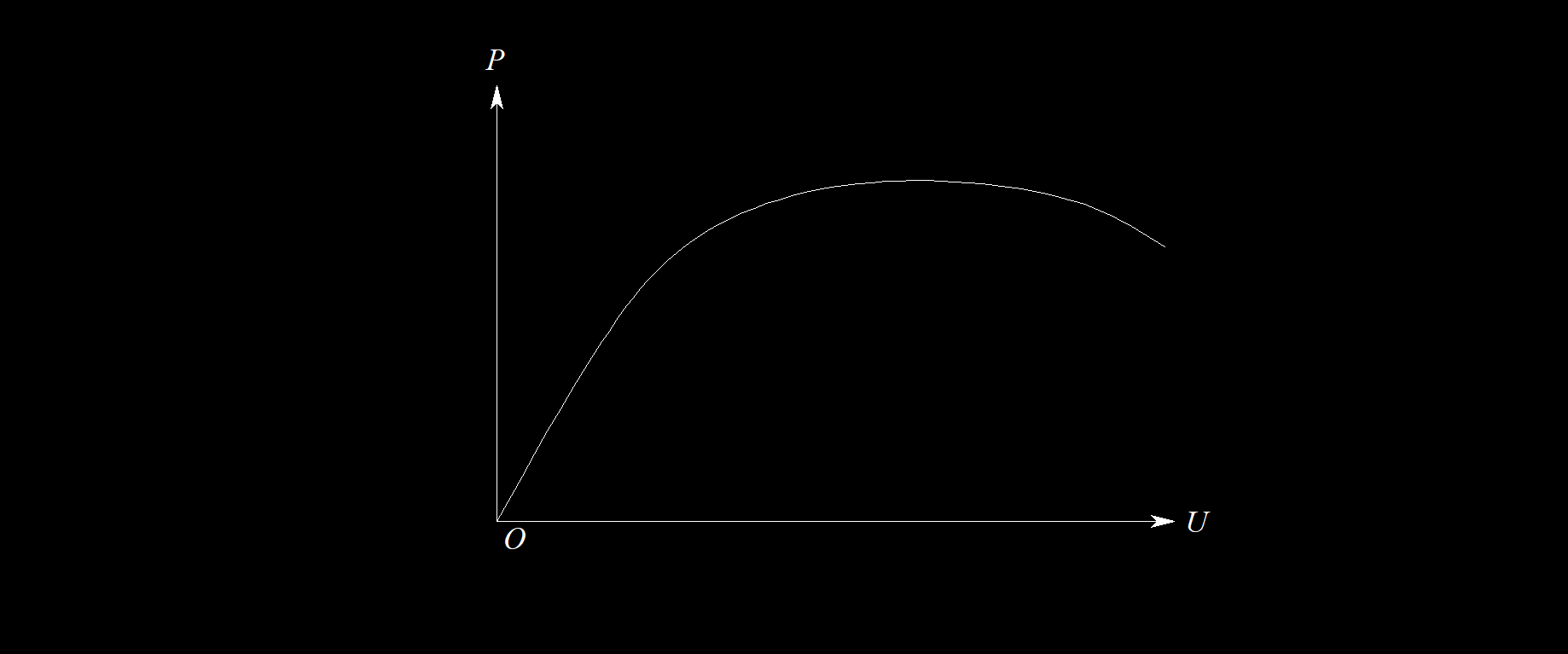
上述是极值点失稳，在陈骥所编《钢结构稳定理论与设计》第五版一书中将钢结构失稳分为三类：
（1）分叉失稳；
（2）极值点失稳；
（3）跃越失稳。
这其中，第2页图1.2（b）应该是有问题的，因为没看到切线刚度小于或等于0的点。
一般我们知道受拉构件是不存在失稳问题的，但是从某种程度上来说其实可以认为是是有的。
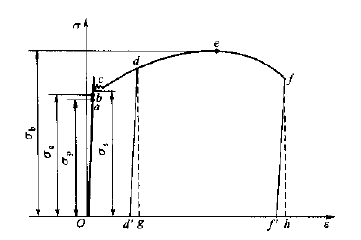
下图是刘鸿文《材料力学》第四版中低碳钢的轴拉荷载变形曲线。可以看到实际上是有极值点和下降段的，也就是说对于拉杆而言，最后的e点其实就是失去稳定了，只是说采用了另一种概念抗拉强度。而对于同样的杆件受压而言，则很有可能极值点出现在屈服点之前，所以相应的稳定会称为显见的问题。
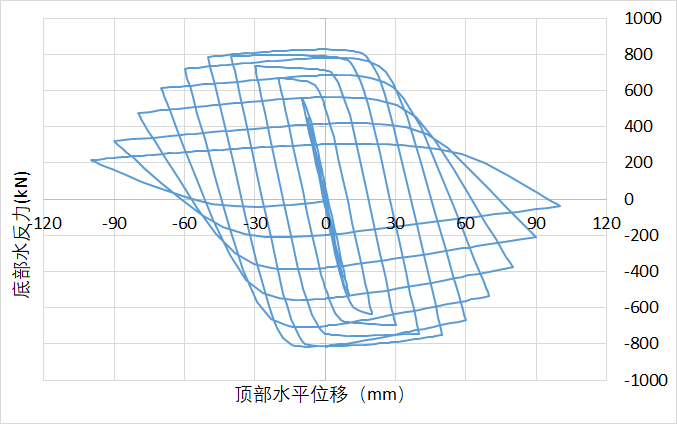
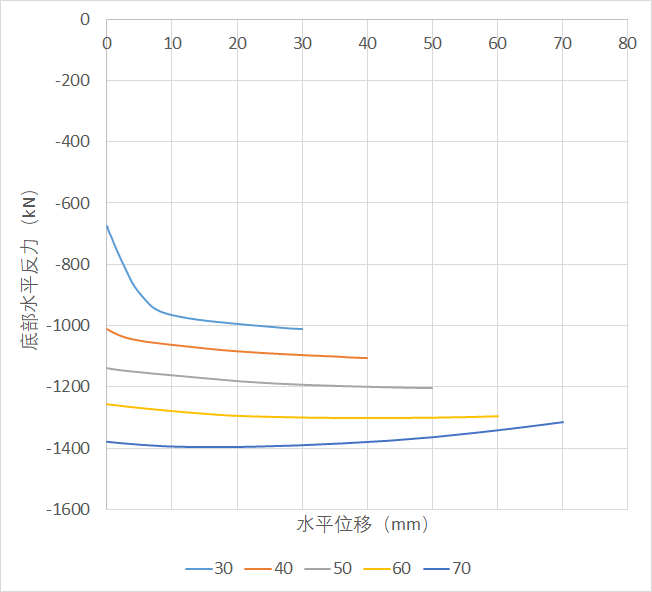
对于滞回曲线而言，每一次正向或反向加载都可视为一次单独的荷载-位移曲线。如果出现了极值点即有下降段，实际上表明已经基本不适合于继续循环加载了。相应的实际上单看骨架曲线上的极值点实际上是有问题的。以下面一组滞回曲线和骨架曲线为例，骨架曲线中可以看到大约50mm水平位移时达到峰值，但是事实上此时已在滞回曲线的下降段。真正的上升段应该只能是取到40mm。因此出现下降段后再去比较和实际上就没什么意义了。
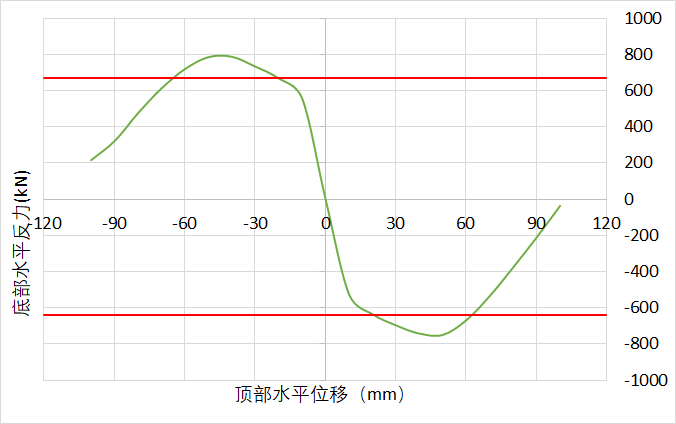
下面是某滞回曲线不同正向位移下反力-位移曲线，可以看到当拉到60mm后，在水平位移70mm这一段内，荷载先上升后下降，尽管终点荷载依旧比60mm时大，但由于出现下降段，相当于在经历了前面的往复加载后，此时已无法加到70mm。
基于上述的分析，再来看几个概念：
（1）屈曲和失稳：如果屈曲后荷载-位移曲线依旧处于上升阶段，那么实际上并不会失稳，也就是说是可以利用屈曲后强度的。换句话说屈曲很有可能发生在极值点之前。
（2）就是承载能力极限状态的问题。
《钢结构设计标准》GB 50017-2017 3.1.3条：
承载能力极限状态应包括：构件或连接的强度破坏、脆性断裂，因过度变形而不适用于继续承载，结构或构件丧失稳定，结构转变为机动体系和结构倾覆。
在《混凝土结构设计规范》GB 50009-2010(2015年版) 6.2.1条条文说明：
纵向受拉钢筋的极限拉应变本规范规定为0.01，作为构件达到承载能力极限状态的标志之一。对有物理屈服点的钢筋，该值相当于钢筋应变进入了屈服台阶；对无屈服点的钢筋，设计所用的强度是以条件屈服点为依据的。极限拉应变的规定是限制钢筋的强化强度，同时，也表示设计采用的钢筋的极限拉应变不得小于0.01，以保证结构构件具有必要的延性。对预应力混凝土结构构件，其极限拉应变应从混凝土消压时的预应力筋应力处开始算起。 对非均匀受压构件，混凝土的极限压应变达到εcu或者受拉钢筋的极限拉应变达到0.01，即这两个极限应变中只要具备其中一个，就标志着构件达到了承载能力极限状态。
可以看到对于变形控制其实是相当严格的。两者都相当于以屈服作为其中一种极限状态的。
（3）如何看待延性
如果荷载超过了峰值荷载，那么显然是会发生破坏的，但破坏的过程会是如何。如果假定荷载逐渐增大施加的，且在到达极值点前遵循荷载-位移曲线，那么延性好的所产生的变形就大。
（4）“大震不倒”又是如何控制的呢？
《建筑抗震设计规范》GB 50011-2010（2016版）1.0.1条条文说明：
遭遇第三水准烈度——最大预估烈度（罕遇地震）影响时，结构有较大的非弹性变形，但应控制在规定的范围内，以免倒塌。
理论上并不需要对变形进行控制，只要不倒，变形多大又有什么关系。但是，地震作用下往复运动会降低极限荷载，相应的控制变形保证承载能力不至于下降太多以致破坏。而构件、结构自身的抗震延性则决定了变形控制的水平。
但是在对构件控制其多次往复加载后承载能力下降多少合适则很难说，因为你无法确定罕遇地震下地震作用到底会有多大。
[1] 对于Ляпунов一阶近似理论可参见梅凤翔等著《约束力学系统运动稳定性》第一版1.3.2节。对于这个理论的更多应用是出现在我的博士论文中。
在《钢结构连接节点设计手册》中，对于对接接头的全熔透焊缝，提到如果轴力与焊缝夹角满足tanθ≤1.5\tan\theta\leq 1.5，则采用三级焊缝也满足要求。但书里并没有提到这一点。……