资治通鉴（摘录2）
卫鞅欲变法，秦人不悦。卫鞅言于秦孝公曰：“夫民不可与虑始，而可与乐成。论至德者不和于俗，成大功者不谋于众。是以圣人苟可以强国，不法其故。”甘龙曰：“不然。缘法而治者，吏习而民安之。”卫鞅曰：“常人安于故俗，学者溺于所闻，以此两者，居官守法可也，非所与论于法之外也。智者作法，愚者制焉；贤者更礼，不肖者拘焉。”公曰：“善。”以卫鞅为左庶长，卒定变法之令。令民为什伍而相收司、连坐，告奸者与斩敌首同赏，不……
一个一直困扰着的问题是为什么会出现锚固长度这一概念，以及其如何计算。事实上连钢混书里都没有讲清楚这一问题。如舒士霖版的书里只讲了“为了使钢筋和混凝土能够可靠地共同工作，钢筋在混凝土中必须要有可靠的锚固。”这句话基本可以视作一句废话吧。没有把锚固为什么能使共同工作讲清楚。……
在编写标准有关于墙与楼板连接时想到了几个问题。
一个一直困扰着的问题是为什么会出现锚固长度这一概念，以及其如何计算。事实上连钢混书里都没有讲清楚这一问题。如舒士霖版的书里只讲了“为了使钢筋和混凝土能够可靠地共同工作，钢筋在混凝土中必须要有可靠的锚固。”这句话基本可以视作一句废话吧。没有把锚固为什么能使共同工作讲清楚。
如下图所示为一拉杆。首先一个假定是钢筋和混凝土之间只能通过摩擦传力，也就是说钢筋的左端头应力应该是0。而按照设计杆内部钢筋应该筋要达到设计强度，那么就需要一个在基础内通过摩擦传递的过程。
图1 实际受力图示
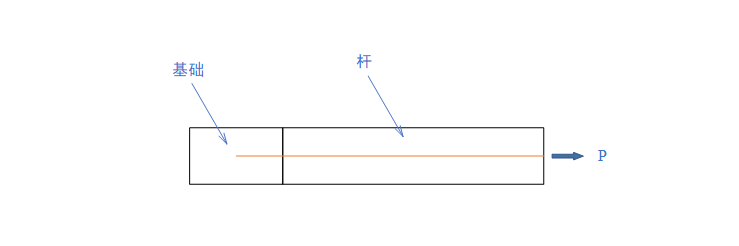
如此锚固长度就是基础内钢筋长度，而要实现这一功能，就需要满足一定长度要求。
在杆和基础交界处钢筋应力为抗拉强度设计值，那么对于这一段传力区间而言钢筋和混凝土接触面上平均应力应该为： 式中：——钢筋截面面积；——钢筋截面周长；——基础内钢筋长度
相应可以得到： 这个形式与规范中的基本锚固长度公式已经一致了。估计不过这里也不是抗拉或抗压强度吧，更应该是抗剪切的。所以要得到规范中的基本锚固长度公式估计也是试验后的经验公式吧。
不过这里有一个问题是杆计算时取多长的问题。如下图所示，计算简图中通常基础是没有尺寸大小的。这样的话如果通长计算就会高估了基础内的承载力。相应的应该根据明确分为两段计算，一是杆，二是基础。基础内部如果不另配筋显然是无法与杆等墙的。
图2 计算简图
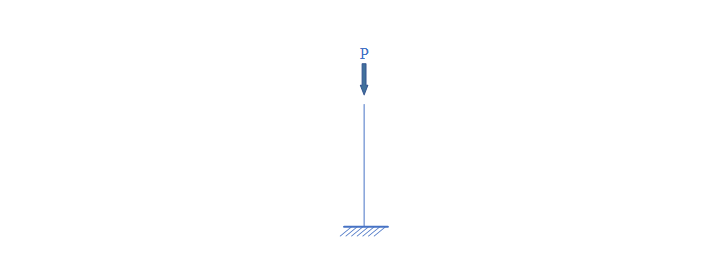
对于梁而言，可能更清楚的说明这个问题。
图3 梁跨度
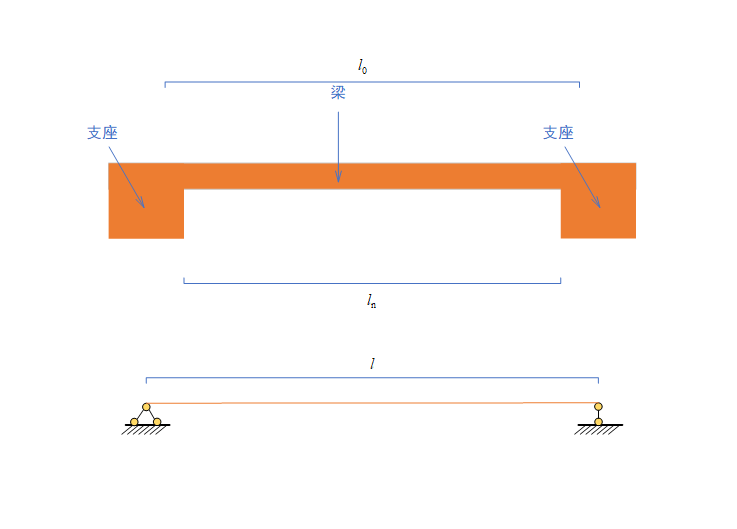
如上图所示，有三种梁跨度。跨度、计算跨度、净跨。由于在一般的配筋图集中锚固长度都是从支座内边缘算起，那么也就是说净跨范围内才是实质性的验算梁承载力的，也是梁根据计算配筋的地方。而理论上如上面所说支座也需要足够配筋。至于计算跨度，则与支座处反力位置有关，不能直接等同于支座中点距离。不过混凝土规范里也没有讲这个计算跨度是如何计算的。
由上面的阐述来分析下新型结构体系楼板支承的问题。首先锚固理论上如果剪力墙腹板两侧都有浇筑混凝土，应该是和混凝土结构一样的。对于边支座或连续板中间支座，支座不考虑弯矩，然后得考虑支座处抗剪的问题（理论上支座处也很难受弯）。考虑等强度的设计方式。混凝土楼板每延米抗剪强度设计值为： 而水平加劲板自身如果采用下述公式作为其抗剪承载力的话： 钢板抗剪强度设计值通常为混凝土抗拉强度设计值的100多倍，那么楼板100多mm厚的话，加劲板基本上只要1~2mm足够了（更不用说是腹板两侧都有加劲板了）。至于焊缝验算等强的话也肯定没有问题。
也就是说，混凝土楼板抗剪强度足够，采用2mm+的加劲板肯定是够了。
回过头来，为什么混凝土楼板不用设箍筋和抗剪验算呢？具体不写了，可参考http://blog.sina.com.cn/s/blog_70d60a4a0102yy1a.html，无非意思是纯无腹筋也远远够了。