高斯积分相关
对于一般的积分表达式，是无法求出其定积分形式的。对于有限元问题而言，主要就是单元刚度矩阵的问题。（当然对于梁单元而言，是可以给出单元刚度矩阵显式表达式的）。因此得用到数值积分方式。而这其中，如果积分具有如下形式，则可以应用高斯积分。……
振型分解法或模态叠加法都可以叫，没有什么区别。实质上就是将位移表达成广义位移的叠加形式，当然前提是线性结构。本文主要讲其方法如何推导及等效静力荷载如何得到。……
振型分解法或模态叠加法都可以叫，没有什么区别。实质上就是将位移表达成广义位移的叠加形式，当然前提是线性结构。本文主要讲其方法如何推导及等效静力荷载如何得到。
《结构动力学》R.克拉夫,J.彭津 王光远等译校
——位移向量
——振型矩阵，这里： 、、——质量矩阵、刚度矩阵、阻尼矩阵
——荷载向量
——地震加速度
——模态阻尼比
——广义位移向量
、——广义质量矩阵、广义刚度矩阵
对于基本的n个自由度体系，有以下运动方程：
考虑自由振动情形：
相应有：
即得式（1）：
此式对于后续将有关键作用。与此同时，可以证明：
（1）正交性 （2）模态频率与广义矩阵关系
（3）单自由度体系简谐荷载稳态解
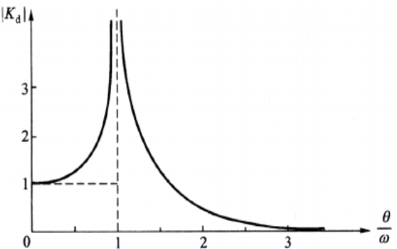
对于多自由度体系，其位移可表示成为：
相应的运动方程转化为：
上述方程两边乘以，得到：
如果阻尼矩阵可以表示成为瑞利阻尼形式，即：
则上述方程进一步简化为：
利用正交性可得广义质量矩阵和广义刚度矩阵均为对角阵，故得到n个单自由度体系方程：
两端除以可以转化为单自由度体系的标准形式，式（2）：
这里基于上式可以求得各阶广义位移。
如果振型向量关于质量矩阵归一化，即：
则式（2）变为：
相应稳态振动解为：
等效静力荷载即产生相同位移时作用的静力荷载值：
代入式（1）可得式（4）：
也就是说在基于单自由度体系求得各阶广义位移后，可以相应得到等效静力荷载。与此同时，等效静力荷载为各阶等效静力荷载的线性叠加，也是一个随时间变化量。
注意到：上述推导过程中质量矩阵和刚度矩阵并不需要是对角阵。
应用1：假定作用一个简谐荷载，那么为什么一般频率较低时相应激发起的位移较大，而即使与相应自振频率差值差不多的情况下。对于这个问题，通过计算可以发现，主要是因为式（3）中分母频率项的原因。譬如：某两阶自振频率是1.05Hz和100.05Hz，相应激励荷载频率分别为1Hz和100Hz，那么前者主要激发的是1.05Hz的模态，此时:
后者主要激发的是100.05Hz的模态，此时：
在差别不大的情况下，相应位移基本是有97.56倍的差别。由此可以看出高频激励相对位移较小（当然这是在频率差值一定的情况下）。